동적 계획법을 지난 시간에 배웠으니, 그에 맞는 문제를 풀어보려 한다.
백준의 실버3 난이도 DP 알고리즘을 쓰는 '2579번 : 계단 오르기' 문제이다.
문제 규칙
이 문제에서는 규칙을 문제 설명에 명시해 두었다.
- 계단은 한 번에 한 계단씩 또는 두 계단씩 오를 수 있다. 즉, 한 계단을 밟으면서 이어서 다음 계단이나, 다음다음 계단으로 오를 수 있다.
- 연속된 세 개의 계단을 모두 밟아서는 안 된다. 단, 시작점은 계단에 포함되지 않는다.
- 마지막 도착 계단은 반드시 밟아야 한다.
동작 원리의 핵심은 2번에 있다.
세 개의 계단을 연속되게 밟으면 안 되고, 한 번에 세 칸 이상씩은 이동할 수 없다는 점이다.
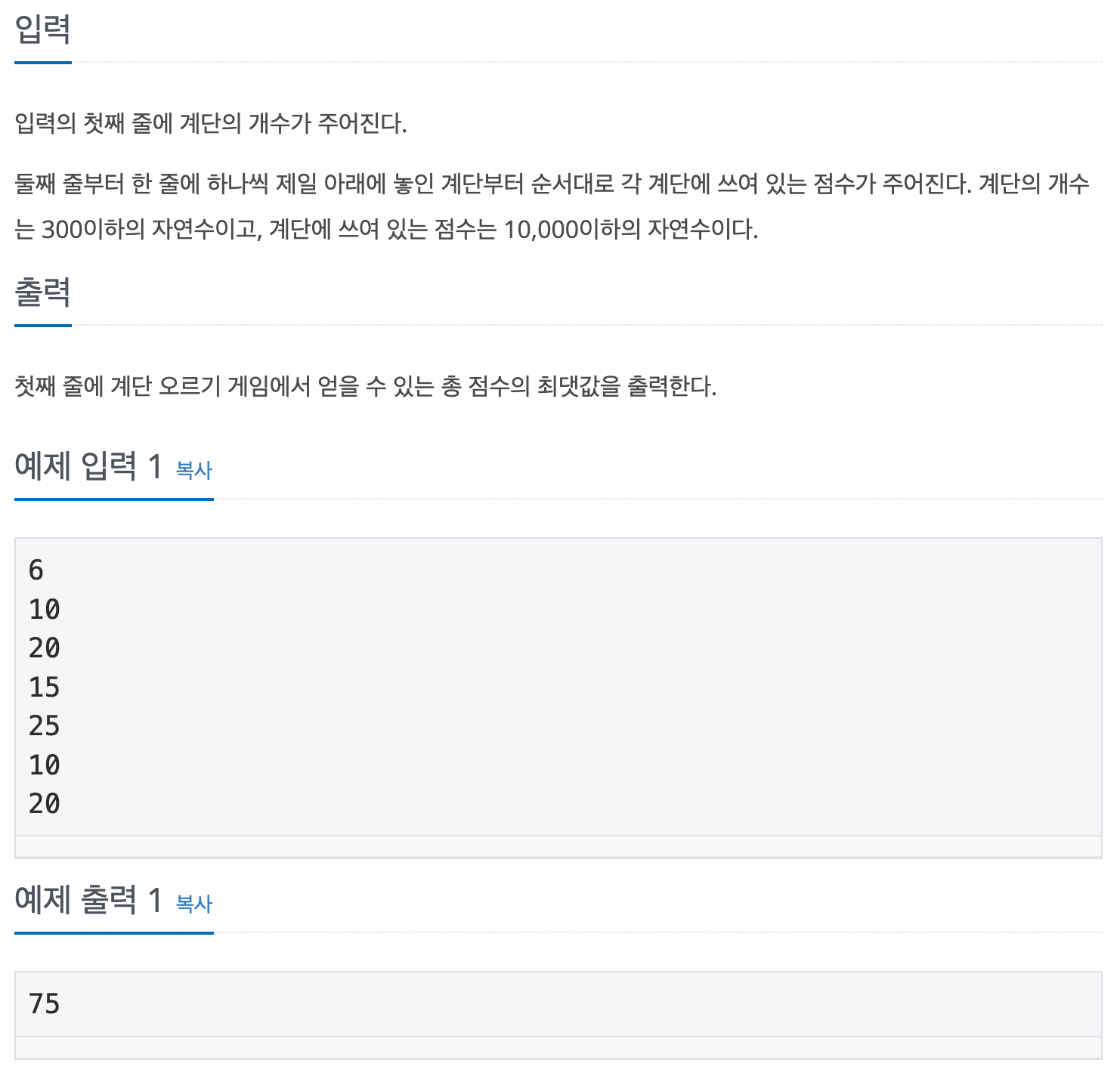
백준에 나와있는 입력 예제이다. 첫 번째 int 변수 n에 계단 개수를 받아주고 계단의 값을 담아줄 arr 배열을 만들어준다.
더불어 이미 계산했던 값을 저장할 cache 배열까지 만들어줄 것이다.
점화식 유도
그럼 그림을 보고 점화식을 유도해 보자

한 번에 3칸 이상 이동할 수 없다는 점을 기억하자
그리고 연속되게 세 칸도 이동할 수 없다.
그럼, n 번째 계단에 도달하려면 경우의 수가 n-3 -> n-1 -> n 과 n-2 -> n 총 두 가지의 방법이 있다.
이를 토대로 점화식을 다음과 같이 정의해 보자
cache[n] = Math.max(cache[n-3] + arr[n-1], cache[n-2]) + arr[n];cache[n] = Math.max(1, 2)를 하면 1, 2 중에 큰 값이 배열 n번째 인덱스에 저장되는 방식이다.
탑다운 방식 (Top-down)
위 점화식을 토대로 탑다운 방식(Top-down)을 이용하여 코드를 작성해 보았다.
import java.util.Scanner;
public class Main {
static int[] cache;
static int[] arr;
public static int dp(int n){
if(n == 1) return cache[1] = arr[1];
if(n == 2) return cache[2] = arr[1] + arr[2];
if(n == 3) return cache[3] = Math.max(arr[1], arr[2]) + arr[3];
if(cache[n] !=0) return cache[n];
cache[n] = Math.max(dp(n-3) + arr[n-1], dp(n-2)) + arr[n];
return cache[n];
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
cache = new int[n+1];
arr = new int[n+1];
for(int i=1; i<=n; i++){
arr[i] = sc.nextInt();
}
System.out.println(dp(n));
}
}탑다운 방식을 사용하여 순환적 알고리즘으로 동작하고, n-3의 경우까지 고려해야 하기에 if문 3개로 종료문을 지정해 주었다.
위 코드에서 핵심은 if(cache[n] != 0) return cache[n];이다.
이미 계산한 값을 저장하는 배열이 원래 0으로 모두 초기화되어 있지만, 0이 아니라면 계산을 했다는 의미이므로 그 값을 바로 불러오게끔 DP 방식을 이용하여 시간초과를 막을 수 있었다.
바텀업 방식(Bottom-up)
다음은 바텀업 방식(Bottom-up) 방식이다.
import java.util.Scanner;
public class Main {
static int[] cache;
static int[] arr;
public static int dp(int n) {
if (n == 1) return arr[1];
cache[1] = arr[1];
cache[2] = arr[1] + arr[2];
cache[3] = Math.max(arr[1], arr[2]) + arr[3];
for (int i = 4; i <= n; i++) {
cache[i] = Math.max(cache[i - 3] + arr[i - 1], cache[i - 2]) + arr[i];
}
return cache[n];
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
cache = new int[n + 2];
arr = new int[n + 2];
for (int i = 1; i <= n; i++) {
arr[i] = sc.nextInt();
}
System.out.println(dp(n));
}
}배열 길이를 신경 써주는 것이 꽤 어려웠다.
'🖥️ Computer Science > Algorithm' 카테고리의 다른 글
| [백준] 7576, 토마토 (Swift) (0) | 2024.02.13 |
|---|---|
| [백준] 2644, 촌수계산(C++, BFS) (1) | 2023.09.02 |
| [백준] 13414, 수강신청 (C++, 해시맵) (0) | 2023.08.10 |
| [C언어] 표준 입력 함수, scanf() 함수의 오류 찾기 (0) | 2023.05.31 |
| [알고리즘] DP(Dynamic Programming) 동적 계획법 (0) | 2023.05.24 |