그래프란 ?
: 정점(Vertex)과 그 정점을 잇는 간선(edge)으로 구성되어 있는 자료구조

무방향 그래프 : 간선의 방향이 없는 그래프
방향 그래프 : 간선의 방향이 있는 그래프
그래프를 표현하는 두 가지 방법
1. 인접행렬
2. 인접리스트
- 인접행렬 표현법 (무방향과 방향 그래프)


무방향 그래프를 인접행렬로 표현하면 대칭적인 형태를 볼 수 있다.
인접행렬을 작성하는 코드는 다음과 같다.
// 그래프의 인접행렬 생성 함수
void createGraph(int arr[][MAX_SIZE], int vertex, int edge) {
int start, destination;
// 인접행렬 초기화
for (int i = 0; i < vertex; i++) {
for (int j = 0; j < vertex; j++) {
arr[i][j] = 0;
}
}
// 간선 정보 입력
for (int i = 0; i < edge; i++) {
printf("간선 %d 입력 (출발지 도착지): ", i + 1);
scanf("%d %d", &start, &destination);
// 유효한 정점 범위인지 확인
if (start >= 0 && start < vertex && destination >= 0 && destination < vertex) {
arr[start][destination] = arr[destination][start] = 1;
// 무방향 그래프의 경우 반대 방향도 1로 설정
}
else {
printf("유효하지 않은 정점입니다.\\n");
i--; // 잘못된 간선 입력이 있을 경우, 다시 입력하도록 i를 감소시킴
}
}
}
차수 구하기
차수란 '각 정점에 연결된 간선의 총 개수'이다.
무방향 그래프의 차수를 구하는 코드
//각 정점의 차수 구하기
for(int i=0; i<n; i++){
degree = 0;
for(int j=0; j<n; j++){
degree += arr[i][j];
}
printf("%d %d\\n", i, degree);
}방향 그래프의 차수를 구하는 코드
// 각 정점의 차수 구하기
for (int i = 0; i < vertex; i++) {
outdegree = 0;
indegree = 0;
for (int j = 0; j < vertex; j++) {
outdegree += arr[i][j]; // 출발하는 간선 개수 (출발 정점의 차수)
indegree += arr[j][i]; // 도착하는 간선 개수 (도착 정점의 차수)
}
printf("정점 %d: 진출 차수 = %d, 진입 차수 = %d\\n", i, outdegree, indegree);
}
무방향 그래프 C언어 구현
각 정점의 차수와 인접행렬을 나타내고 있다.
#include <stdio.h>
#define MAX_SIZE 100
// 그래프의 인접행렬 생성 함수
void createGraph(int arr[][MAX_SIZE], int vertex, int edge) {
int start, destination;
// 인접행렬 초기화
for (int i = 0; i < vertex; i++) {
for (int j = 0; j < vertex; j++) {
arr[i][j] = 0;
}
}
// 간선 정보 입력
for (int i = 0; i < edge; i++) {
printf("간선 %d 입력 (출발지 도착지): ", i + 1);
scanf("%d %d", &start, &destination);
// 유효한 정점 범위인지 확인
if (start >= 0 && start < vertex && destination >= 0 && destination < vertex) {
arr[start][destination] = arr[destination][start] = 1;
// 무방향 그래프의 경우 반대 방향도 1로 설정
}
else {
printf("유효하지 않은 정점입니다.\\n");
i--; // 잘못된 간선 입력이 있을 경우, 다시 입력하도록 i를 감소시킴
}
}
}
// 인접행렬 출력 함수
void displayGraph(int arr[][MAX_SIZE], int vertex) {
int i, j, degree;
//각 정점의 차수 구하기
for (int i = 0; i < vertex; i++) {
degree = 0;
for (int j = 0; j < vertex; j++) {
degree += arr[i][j];
}
printf("%d: %d\\n", i, degree);
}
//인접행렬 나타내기
printf("\\n인접행렬:\\n");
for (i = 0; i < vertex; i++) {
for (j = 0; j < vertex; j++) {
printf("%d ", arr[i][j]);
}
printf("\\n");
}
}
int main(void) {
int vertex, edge;
int arr[MAX_SIZE][MAX_SIZE] = { 0 };
printf("정점의 개수를 입력하세요: ");
scanf("%d", &vertex);
printf("간선의 개수를 입력하세요: ");
scanf("%d", &edge);
createGraph(arr, vertex, edge);
displayGraph(arr, vertex);
return 0;
}
만일 방향 그래프를 구현하고 싶다면 createGraph 함수에서 아래처럼 코드를 수정한다. (차수 구하는 것도 수정 필요)
arr[start][destination] = arr[destination][start] = 1
↓
arr[start][destination] = 1
인접리스트 표현

위 사진은 무방향 그래프를 인접리스트로 만든 사진이며
구조체 G_node List 배열의 인덱스가 각각의 연결된 정점들을 연결리스트로 이은 방식이다.
다음은 방향 그래프를 인접리스트로 만든 모습이다.
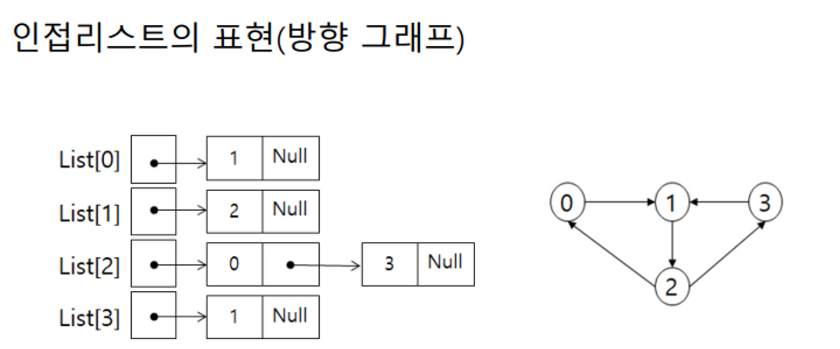
인접행렬을 인접리스트로 바꾸기
#include <stdio.h>
#include <stdlib.h>
#define MAX_SIZE 100
typedef struct node {
int vertex;
struct node* link;
} G_Node;
void Adj_insert(G_Node** List, int i, int j) {
G_Node* newnode = (G_Node*)malloc(sizeof(G_Node));
newnode->vertex = j;
newnode->link = List[i];
List[i] = newnode;
}
void Adjmat2list(G_Node* List[], int arr[][MAX_SIZE], int vertex) {
for (int i = 0; i < vertex; i++) {
for (int j = 0; j < vertex; j++) {
if (arr[i][j] == 1) {
Adj_insert(List, i, j);
}
}
}
}
void Display(G_Node* List) {
G_Node* cur = List;
while (cur != NULL) {
printf("%d -> ", cur->vertex);
cur = cur->link;
}
printf("NULL\\n");
}
int main() {
int vertex, edge;
printf("정점의 개수를 입력하세요: ");
scanf("%d", &vertex);
int arr[MAX_SIZE][MAX_SIZE] = { 0 };
printf("간선의 개수를 입력하세요: ");
scanf("%d", &edge);
for (int i = 0; i < edge; i++) {
int start, destination;
printf("간선 %d 입력 (출발지 도착지): ", i + 1);
scanf("%d %d", &start, &destination);
// 유효한 정점 범위인지 확인
if (start >= 0 && start < vertex && destination >= 0 && destination < vertex) {
arr[start][destination] = 1;
}
else {
printf("유효하지 않은 정점입니다.\\n");
i--;
}
}
G_Node* List[MAX_SIZE] = { NULL };
Adjmat2list(List, arr, vertex);
for (int i = 0; i < vertex; i++) {
printf("List[%d]: ", i);
Display(List[i]);
}
return 0;
}
수행시간 분석
마지막으로 위 개념들의 수행시간을 분석해 보면
인접행렬로 표현한 경우 2차원의 행렬이므로 수행시간은 최소 O(n^2)이다.
인접리스트로 표현한 경우 연결 리스트를 이용하였으므로 수행시간은 최소 O(노드 수 + 간선 수)이다.
이상 그래프의 기초 개념이다.
다음은 그래프와 트리에 관해 이야기 하며 응용해 보겠다.
'🖥️ Computer Science > Data Structure' 카테고리의 다른 글
| [메이드 인 스위프트] 자료구조 - 큐 Queue 구현해보기 (0) | 2024.12.27 |
|---|---|
| [메이드 인 스위프트] 자료구조 - 스택 Stack 구현해보기 (0) | 2024.12.25 |
| 그래프 응용(최소신장트리), Prim 알고리즘 C언어 구현 (0) | 2023.05.27 |
